Option Greeks are a set of metrics that measure the sensitivity of an option’s price to various factors. They help traders and portfolio managers assess and manage the risks associated with options.

Theta: Sensitivity to Time

Theta measures the rate of change of an option’s price with respect to the passage of time (time decay).

Example: A Theta of -0.02 means the option loses $0.02 in value every day, all else being equal.

Uses: Assessing the impact of time decay for an option, especially for short-term options.

Ranges: Long options always has negative theta, short options always have positive theta (Regardless of whether it is put or call).

Time Decay: Time value of an option decrease over time in a non-linear manner. The time decay accelerates when getting closer to expiration, till the time value reaches zero.

• If you hold a long position on a option, time is your ememy. As days progress, you loss time value gradually.
• If you hold a short position on a option, time is your friend. Vice versa.

Option Price = Time Value + Instrinstic Value; Although the time decay will reduce the time value of an option over time, it will have no impact on the instrinic value of the option.

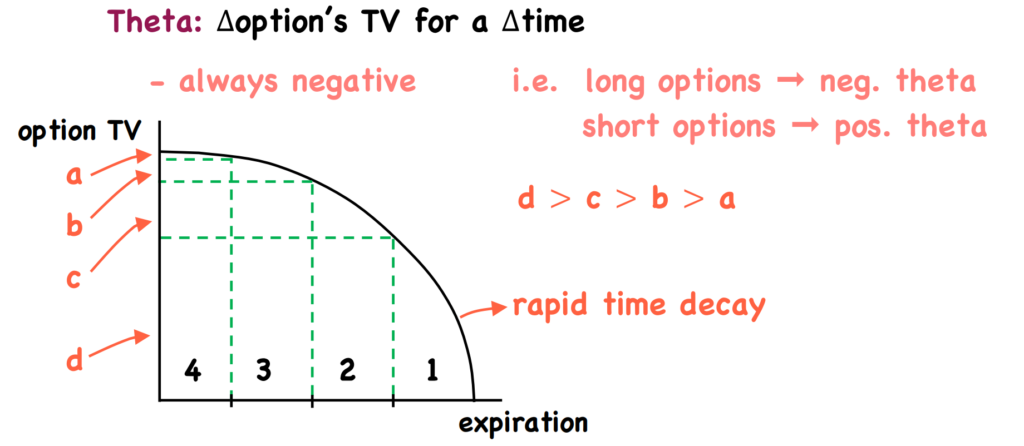
How to play with time (General time strategies): Looking at the graph with x axis as time till expiration, y axis as the time value of the option. Assumes this graph represent a call option.

• Since the time decay faster when near expiration, we can utilises this when selecting which call option to buy.
• Suppose we want to long a call, and sell it after a month.
• Long a call with 4 months till expiration and sell it at 3 months left(Sell it after a month).
• The time value of the option will not decay much, represented by segment a. That means the call option retains most of its time value, make this call option preferable to sell.
• However, if you long a call with 1 month till expiration, 1 month later the time value of the option will decay to 0 at expiration. Segment d represents larger time values lost due to increasing time decay near expiration.
• Therefore, long near expiration calls is not preferable, but you can choose to short near option options.

Summary:

• For long options: Buy more time than required. (Buy 4 months to expiration option, not 1 month)
• For short options: Sell more time than required. (Sell 1 month to expiration option, not 4 months)

Vega: Sensitivity to Volatility

Vega measures the change in the option’s time value for a change in the volatility of the underlying.

Notice that Vega measures the change in the time value not the whole option value (time value + intrinsic value). Let use a example to illustrate why:

• Suppose we long a call at strike price(X) of $10 and spot price(S) is $20.
• Assumes the volatility of the underlying is 10% initially and increase to 30%.
• The intrinsic value of the stock is S – X = 20 – 10 = $10, which will not be affected by change in volatility.
• However, time value will increase as volatility increases.

Ranges: The long options always have positive vega, short options always have negative vega. This is because the volatility itself is always going to be positive for an underlying.

Cv = Pv at X: The Vega of a call and put option is equal when at same strike price. However, it does not mean the implied volatility of the call and put option is the same(C𝛔 != P𝛔).

Rho: Sensitivity to Interest Rate

Rho measures the change in option’s time value for a change in interest rate.

Dynamics: As interest rate increases, the call option price increases, the put option price decreases. When r = 0, call equal to put option price if spot price is at strike price

Ranges: Call options have Rho > 0, puts have Rho < 0