To save or not to save, that is the question.
Two-period consumption saving model:
Asumptions:
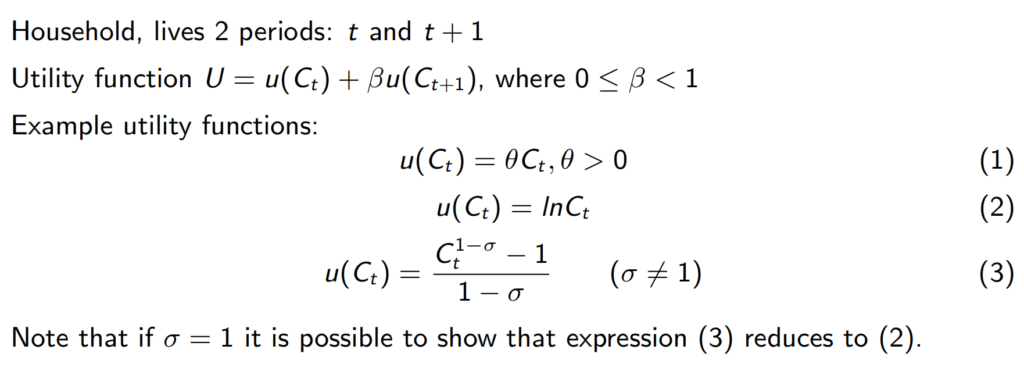
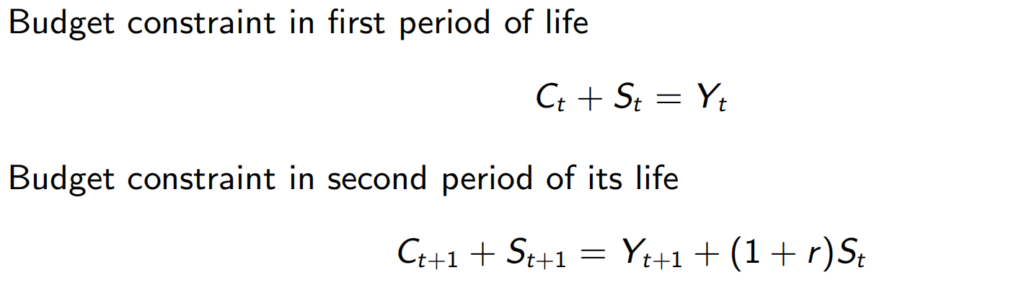

An example:
- Assumes the price of consumption goods in the first period is 1;
- Then the price of the consumption in second period is 1/(1+r)
Consumption Optimisation using the Euler equation:

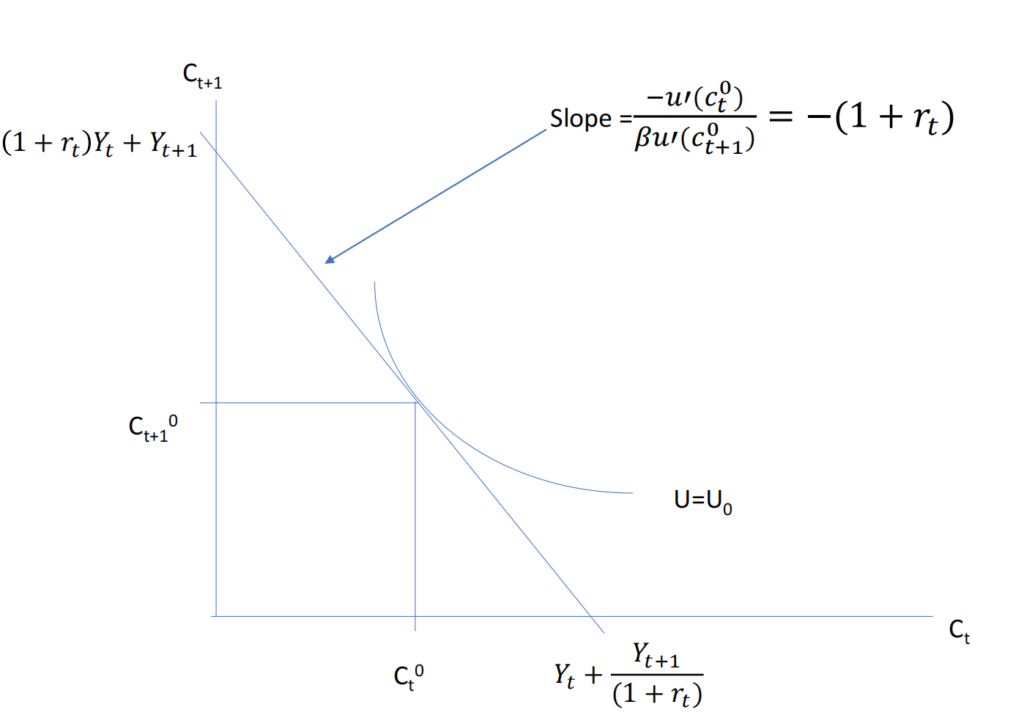
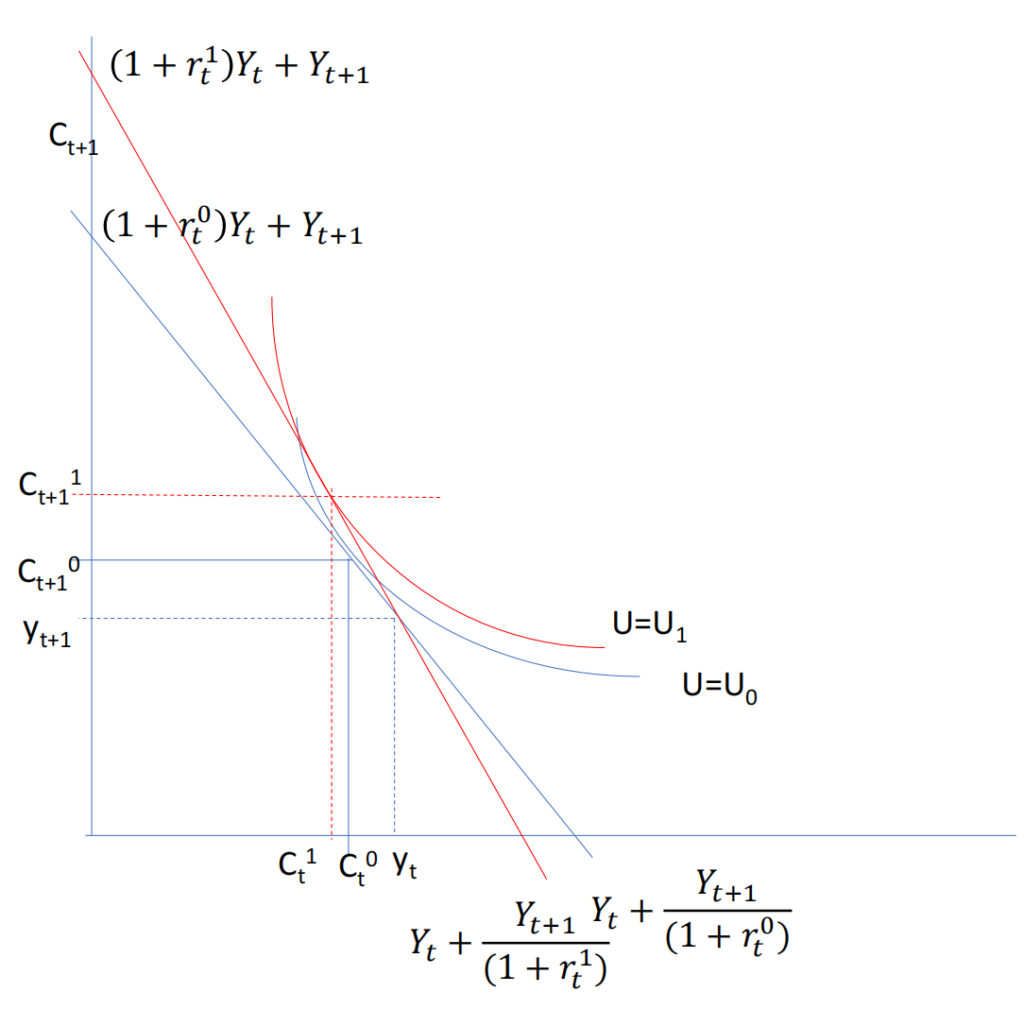
Euler Equation is about the finding out the optimal allocation of consumption. When the marginal rate of substitution equal to the relative price of consumption -(1+r), you find the optimal consumption allocation at where
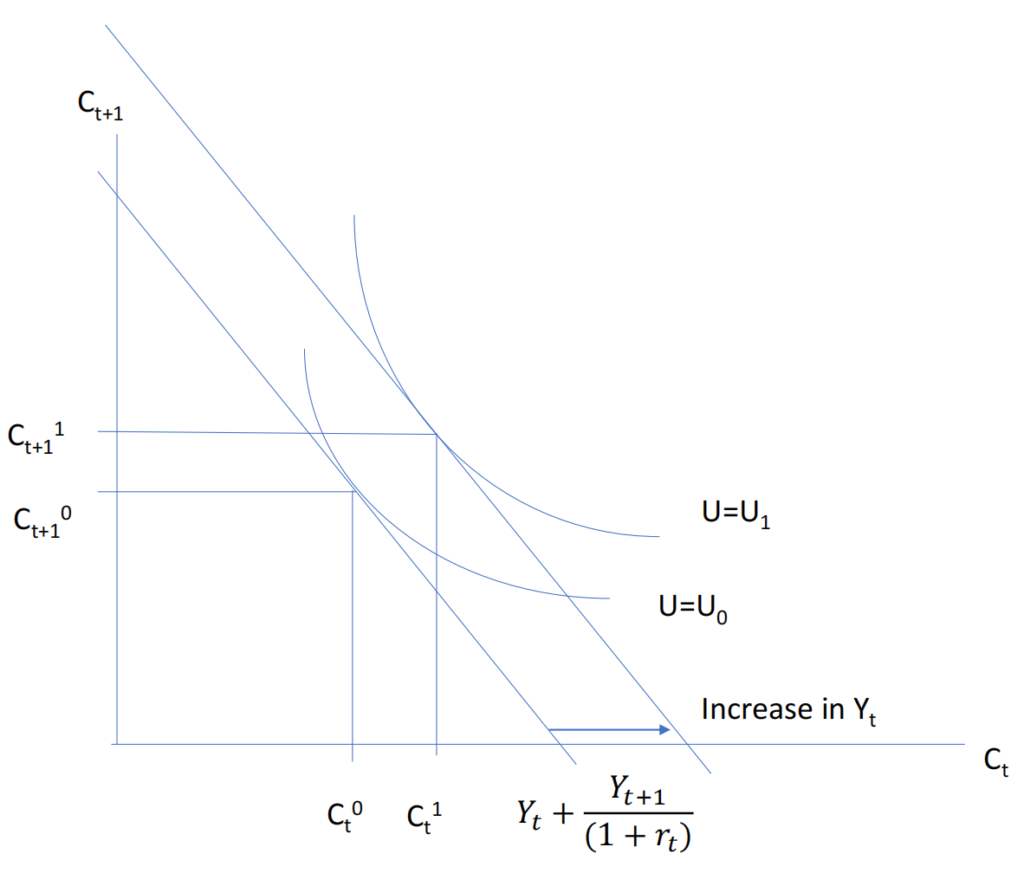
An increase in either period 1 or period 2 income will shifts the budget line outwards. If the consumption is for a normal goods then the consumption rises in both period. The relative price of consumption in t+1 to t is unchanged as it only depends on interest rate. The original endowment point is at Ct0,Ct+10 and it lies on lower intertemporal budget constraint. With increase in income it shifts the budget constraints with the endowment point to a higher level.
An increase in the interest rate will pivot the budget line to be steeper. As the future consumption will be cheaper and is substitued for current consumption. The will be a negative substitution effect which reduces the current consumption.
If income is accrued mainly in first period then people would increase their consumption in both periods due to a sufficiently large positive income effect. If income accrued mainly in period 2, then the income effect would depress consumption in both periods.
Interest rate elasticity of saving:

Notice the bigger the σ, the more concave the utility function, which make consumption less sensitive to change in interest rate. When σ = 1, the change in log consumption is equal to the interest rate plus a trend term.
There is also a wealth effect, rising interest rate will cause the present value of future income declines, therefore reducing consumption in the present and the future. This concepts is really similar to the DCF for sell-side valuation, where if the discount rate is higher, the valuation would be lower.
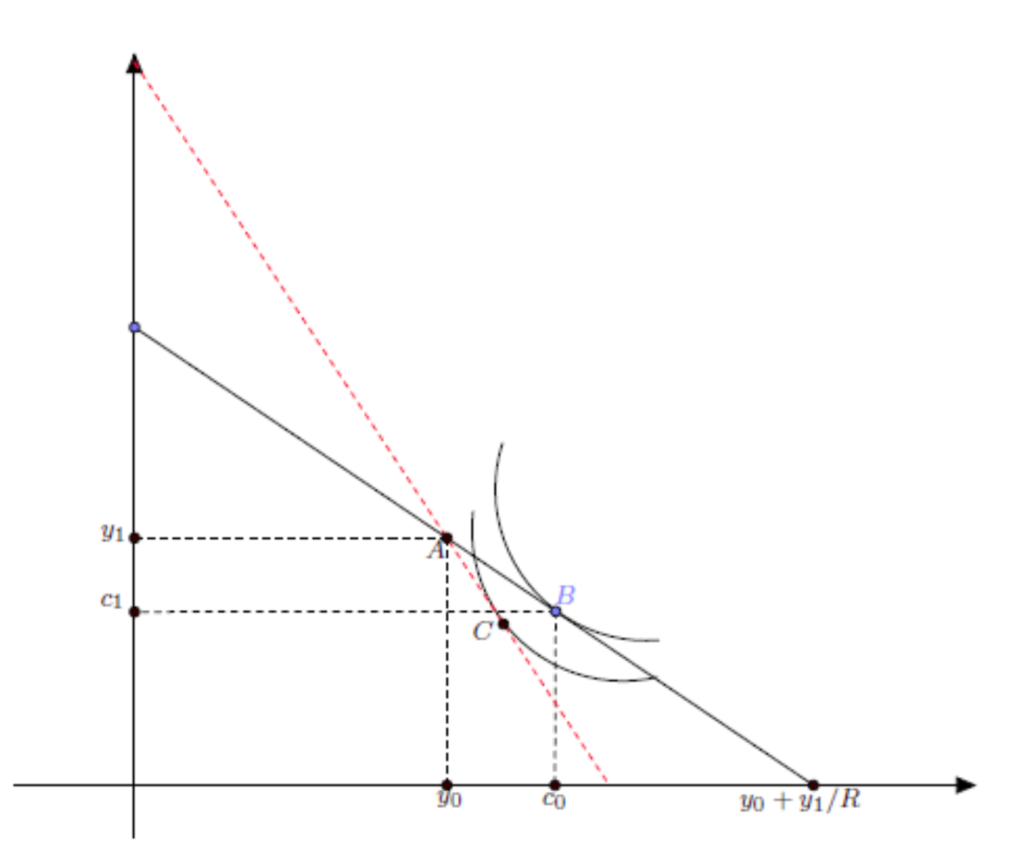
Case 1: If you are borrower, and there is an increase in the interest rate
- Initially you are starting at endowment point A, y1 and y0;
- As you prefered to spend it now more, your consumption is B at c1 and c0;
- Notice that y1 > c1 and y0 < c1, which is different from our origal assumption where they are both equal.
- An rate hike would shift you from B to C, due to negative substitution and income effect for present consumption. You did not benefit from the rate hike as you prefer not to save for future consumption.
Adding Uncertainty to our Model:


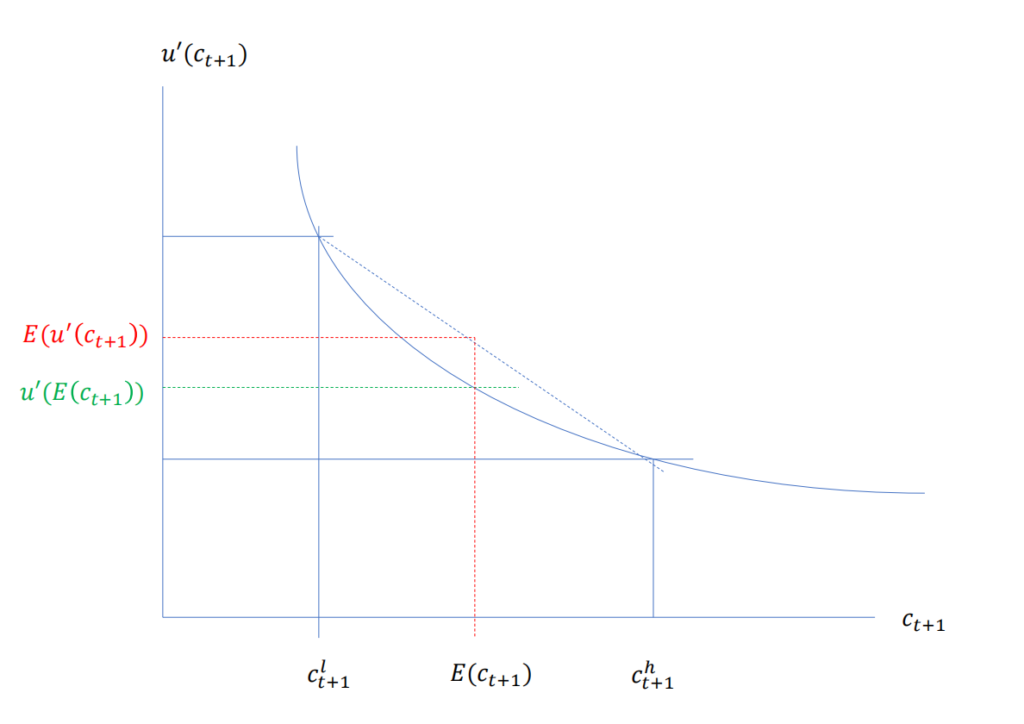
Notice that the expected value of the marginal utility is bigger than the marginal utility of the expected consumption. The former is a linear combination which take the weighted average of the two points a convex utility curve. The latter is selecting a tangent point on the convex utility curve which takes expected consumpation as an input.
Now we can add more complexity to our model
A multi-period consumption-saving model
Asssumptions:


If beta * (1+r) = 1: where we may be impatient on saving more, but driven by high interest rate; so that the net effect is offseted.


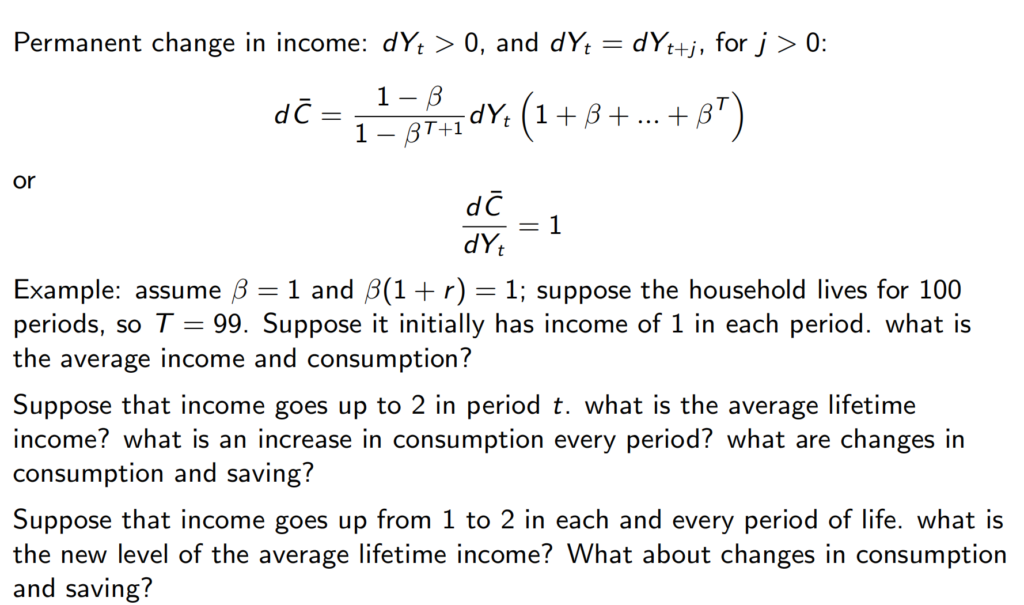
Ans:
If the Beta = 1, and r = 0; Every period’s cash flow would be exactly the same; hence the average income = average consumption = 1
If income goes up only in one particular period, but not in the rest of the period; then the impact on the consumption is neglible.
If income goes up in all periods, then the impact would be great.


Leave a Reply