Ques 1: What methods can be used for computing Greeks given a method for computing prices? What are their advantages and disadvantages?
Ans: Three popular methods for computing the Greeks:
- finite-difference approximations
- pathwise method
- likelihood ratio method.
Finite-difference Approximations:
- How it works:
- Computes the price of the option for slightly perturbed inputs (e.g., underlying price, volatility)
- Use the differences between the computed prices to estimate the derivatives.
- For example, computing Delta:
- Delta ≈ [V(S+h)−V(S)]/h
- Where V is the payoff function which transform underlying price(S) to Option value.
- h is a small pertubation in the underlying price S.
| Advantages | Disadvantages |
| Simple to implement: Require only the ability to compute option prices with slightly different inputs. | Computationally Intensive: Requires multiple price evaluations, which can be costly for complex models like Monte Carlo simulations. |
| General Applicability: Can be applied to any model that computes option prices numerically | Accuracy Issues: Sensitive to the choice of h. A very small h can cause numerical instability, while a large h reduces approximation accuracy. |
Pairwise Method:
- How it works:
- Mostly using Monte Carlo Simulations
- First by simulating for different values of θ (small perturbation in underlying price) by first differentating the option’s payoff and then taking the expectation under the risk-neutral measure.
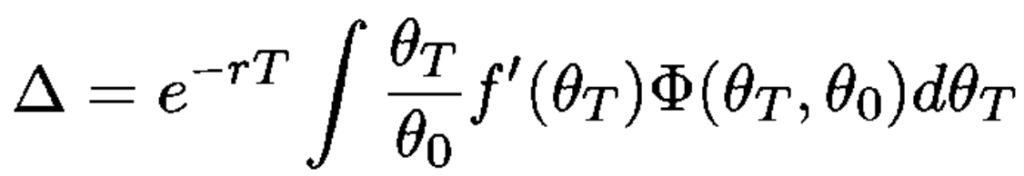
The pairwise method has several advantages: it is an unbiased estimate and only requires simulation for one value of θ and is usually more accurate than a finite-difference approximation.
However, it does become more complicated when the payoff is discontinous (e.g. digital and barrier options, which are exotic options with unique payoff structures that differ from vanilla options like calls and puts). But to get around this we can write f = g + h, with g continous and h piecewise constant.
The likelihood ratio Method:
- How it works:
- The likelihood ratio method is similar to the pairwise method, but instead of differentating the payoff we differentiate the density Φ.
- Where Ψ is the derivative of Φ by θ.
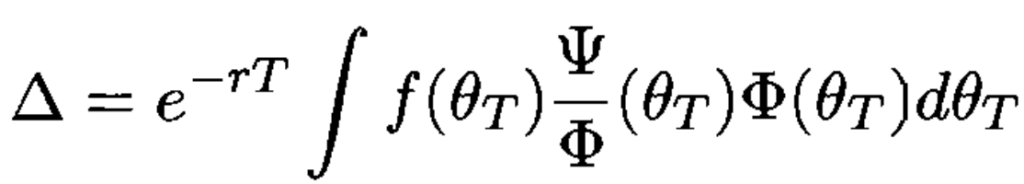
One advantage with the likelihood ratio method is that only one value of θ needs to be simulated to calculate both the price and the sensitivity. No need to worry about discontinuities in the payoff function as we are differentiating the densitity.
However, one drawback is that we need to explicitly know the density.
Ques 2: How does the Gamma of call option vary with time?
Ans: The Gamma for a long position in a vanilla call or put option is always positive. As the option’s maturity approaches, the Gamma will become more spiked at the strike price.
Why does this happen?
- The positivity of Gamma is due to call and put options being convex function of spot as the second derivative for any convex function is positive.
Why does the Gamma become more spiked as maturity approaches?
- If we think about the option’s Delta for short maturities, it will behave almost like a step function, jumping from zero below the strike to one above it. The derivative of Delta will reflect this jump and therefore produces a spiked Gamma.

Ques 3: Suppose an option pays one if spot stays in range K1 to K2 and zero otherwise. What can we say about Vega?
Ans: This option, known as a double no-touch, will have a negative Vega.
- Double No-Touch Option is an exotic derivative contract that pays a fixed amount if the underlying asset’s price stay within a specific range (between two strike prices) for the entire life of the option.
Vega measure the change in option price for a 1% change in volatility. If volatility increases then the probability in the risk-neutral measure of hitting either barrier K1 or K2 increases and so the option price will decrease, giving a negative Vega.
Ques 4: All being equal, which option has higher Vega?
- An at-the-money European call option with spot 100
- An at-the-money European call option with spot 200
In addition: A structurer asked this question and did not want formulas.
Ans: One way to answer this question is to firstly think about how the values of the two options differ. Both of these option are at the money, so doubling the value of the spot will double the strike and hence the value of the option, the factor of two multiplies through. Therefore the option with spot 200 will be worth twice as much as the option with the spot price 100.
The Vega of option B will be twice of the Vega of the option A, as the two will multiply through the Vega as well.
Ques 5: How you construct a Vega neutral portfolio with vanilla call and put options?
Ans: Firstly, we need to know what the current Vega of the portfolio is. The Vega for the portfolio will be the sum of all the individual instrument’s Vegas, so we find these and add them up.
If the value is non-zero we will have to use an option to make it zero. We can either use a call or put as the Vega of a Vanilla call is the same as a put, due to put-call parity and the forward contract having zero Vega.
We take an option which expires at the a similar time to the portfolio and find its Vega. We then buy or sell enough of these options to make the Vega of our portfolio zero.
Ques 6: How accurate do you think a pricing function should be?
Ans: Acuracy is one basis point, which is 0.01%. Another approach is to consider the uncertainty in the inputs. If volatility is estimated rather than observed, an error that is small compared to one Vega is sufficient.
You can also mention that it is error as a fraction of the uncertain part the price that is important, not as a fraction of the total price.
- For example: a deeply in-the-money option is almost all intrinstic, it is the estimate of the value of the optionality tht matters.
Ques 7: Assume you have a good trading model that you think will make money. What information would you present to your manager to support your claim?
Ans: We should think of two models:
- Statistical Arbitrage Model
- A model for pricing exotic derivatives
Statistical Arbitrage involves exploiting small mispricings in the market, usually by buying and selling stocks to create a portfolio which has minimal risk, but potential for profit. This portfolio of stock is often very large, and thus requiring massive compution power. Therefore, one aspect of a good model is that it return trade information in a useful time frame.
What other information would you use to prove your model is a good one? A good check is to back-test the model, seeing how the trades it suggested actually worked on historical data. You can argue that ‘past performance does not imply future result‘. Model that pass the back-test usually fit well with the training and validation data. However, another important test is that it should also work on ‘out of sample’ data, which is external to the training data.
Typically, ‘stab art’ works well in normal times but fails when turbulence occurs. You therefore might want to demonstrate it will still works in a period of turbulance. If you can prove your model can also work in stressed markets, your manager will be happy.
Make sure that u also take into account of:
- Bid-offer spread
- Transaction cost
- Liquidity (use the example of LTCM which fail to meet the liquidity due to its bond arbitrage strategy; LTCM’s main strategy involves longing the cheaper 29.75 year maturity off-the-run Tresury bond and short the 30 year on-the-run bond. It is beting on the yield curve convergece when the on-the-run become off-the-run bond. It captures this slight mispricing and use massive leverge and facing double risk exposure to both long and short position if yield curve diverges; Because of this massive position of using leverage for the off-the-run bond, it is hard to roll off all of it in a short period)
Exotic derivative can also be used. Firstly, you have ensure your model can replicate the price of vanilla options and discount bounds, then the traders will need a lot of convining that it will price exotic instruments correctly.
You should also present what this model does. The model should give outputs:
- option prices
- suggesting a hedging strategy
- provide accurate hedging ratios
Once again if we run back-testing on market data. If the variance of the profit and loss to a trading book is less under you model than the current model, the hedging is more accurate. Congrats!
What your should aim for for your model?
- Speed
- Realisim
- Ease of caliberation
- Ability to easily adjust for new products


Leave a Reply