Black-Schole Model assumes:

• constant volatility
• constant risk-free rate
• It follows a geometric brownian motion
• The underlying intrument is liquid, instant trade execution is available
• Short-selling is permitted
• No market frictions (no transaction cost, regulatory constraints, taxes)
• No arbitrage opportunities are available in the marketplace
• The options are European-style (No early excise)

Ques 1: Derive the Black-Scholes equation for a stock, S. What Boundary conditions are satisfied at S = 0 and S = ∞?

Ans: The evolution of the stock price S_t is given by:

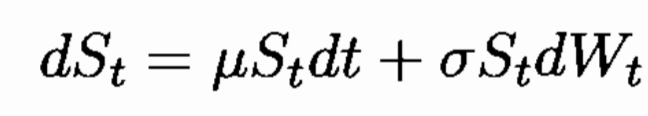
• Also, noted that payoff of a call option: max(S_T – K, 0)

Since, under Black-Scholes, the model assumes no arbitrage exists, therefore, the mean level is set at the risk-free interest rate level.

Ques 2: Derived the Black-Scholes equation so that an undergrad can understand it.

Ques 3: Explain the Black-Sholes equation

Ques 4: Suppose two assets in a Black-Scholes would have the same volatility but different drifts. How will the price of call options on them compare? How suppose one of the assets undergoes downward jumps at random times. How will this affect option prices?

Ques 5: Supppose an asset has an determinstic time dependent volatility. How would I price an option on it using the Black-Scholes Theory? What is the Hedging Strategy?

Ques 6: In the Black-Scholes world, price a European option with a payoff (at time T)

• max (S_T² – K, 0)

Ques 7: Develop a formula for the price of a derivative paying (assuming Black-Scholes model):

• max(S_T (S_T – K), 0)